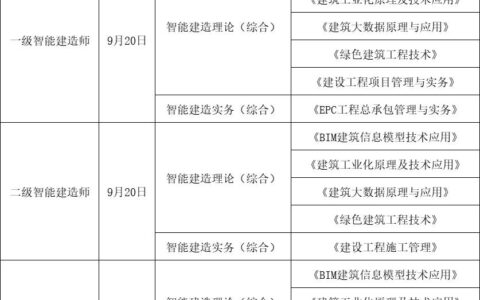
定积分公式运算法则(定积分四则运算法则)

定积分公式运算法则

积分四则运算常用法则：

1）∫0dx=c不定积分的定义

2）∫x^udx=(x^(u+1))/(u+1)+c

3）∫1/xdx=ln|x|+c

4)∫a^xdx=(a^x)/lna+c

5）∫e^xdx=e^x+c

6）∫sinxdx=-cosx+c

积分是微分的逆运算，即知道了函数的导函数，反求原函数。在应用上，积分作用不仅如此，它被大量应用于求和，通俗的说是求曲边三角形的面积，这巧妙的求解方法是积分特殊的性质决定的。主要分为定积分、不定积分以及其他积分。

积分的性质主要有线性性、保号性、极大值极小值、绝对连续性、绝对值积分等。

通常意义上的积分都满足一些基本的性质。以下积分区域在黎曼积分意义上表示一个区间，在勒贝格积分意义下表示一个可测集合。积分的性质有：线性性、保号性、极大值极小值、绝对连续性、绝对值积分等。

线性性积分是线性的。如果一个函数f可积，那么它乘以一个常数后仍然可积。如果函数f和g可积，那么它们的和与差也可积。

定积分四则运算法则

定积分是不具备四则运算的，但是定积分是适合线性运算法则的。四则运算有乘除，线性运算法则只有加减及结合、分配率。定积分是积分的一种，是函数f(x)在区间[a,b]上积分和的极限。这里应注意定积分与不定积分之间的关系：若定积分存在，则它是一个具体的数值，而不定积分是一个函数表达式，它们仅仅在数学上有一个计算关系（牛顿-莱布尼茨公式）。

定积分的几何意义是被积函数与坐标轴围成的面积，x轴之上部分为正，x轴之下部分为负，根据cosx在[0,2π]区间的图像可知，正负面积相等，因此其代数和等于0。

定积分是积分的一种，是函数f(x)在区间[a,b]上的积分和的极限。

这里应注意定积分与不定积分之间的关系：若定积分存在，则它是一个具体的数值（曲边梯形的面积），而不定积分是一个函数表达式，它们仅仅在数学上有一个计算关系（牛顿-莱布尼茨公式），其它一点关系都没有！

一个函数，可以存在不定积分，而不存在定积分；也可以存在定积分，而不存在不定积分。一个连续函数，一定存在定积分和不定积分；若只有有限个间断点，则定积分存在；若有跳跃间断点，则原函数一定不存在，即不定积分一定不存在。

定积分的基本运算法则

求定积分主要的方法有分部积分法和换元积分法。分部积分法是由微分的乘法法则和微积分基本定理推导而来的。它的主要原理是将不易直接求结果的积分形式，转化为等价的易求出结果的积分形式的。分部积分法设u=u(x),v=v（x)均在区间[a,b]上可导，且u′，v′∈R（[a,b]),则有分部积分公式积分是微分的逆运算，即知道了函数的导函数，反求原函数。

在应用上，积分作用不仅如此，它被大量应用于求和，通俗的说是求曲边三角形的面积，这巧妙的求解方法是积分特殊的性质决定的。主要分为定积分、不定积分以及其他积分。积分的性质主要有线性性、保号性、极大值极小值、绝对连续性、绝对值积分等。

定积分的计算公式

具体计算公式参照如图：

扩展资料：

定积分是积分的一种，是函数f(x)在区间[a,b]上的积分和的极限。

积分分类

不定积分（Indefinite integral）

即已知导数求原函数。若F′(x)=f(x)，那么[F(x)+C]′=f(x).(C∈R C为常数).也就是说，把f(x)积分，不一定能得到F(x)，因为F(x)+C的导数也是f(x)（C是任意常数）。所以f(x)积分的结果有无数个，是不确定的。我们一律用F(x)+C代替，这就称为不定积分。即如果一个导数有原函数，那么它就有无

定积分

限多个原函数。

定积分（definite integral）

定积分就是求函数f(X)在区间[a,b]中的图像包围的面积。即由 y=0,x=a,x=b,y=f(X)所围成图形的面积。这个图形称为曲边梯形，特例是曲边三角形。

一个函数，可以存在不定积分，而不存在定积分，也可以存在定积分，而不存在不定积分。一个连续函数，一定存在定积分和不定积分；

若只有有限个间断点，则定积分存在；若有跳跃间断点，则原函数一定不存在，即不定积分一定不存在。

积分在实际问题中的应用

（一）经济问题

某工厂技术人员告诉他的老板某种产品的总产量关于时间的变化率为R′（t）=50+5t-0.6t2，现在老板想知道4个小时内他的工人到底能生产出多少产品。

如果我们假设这段时间为[1，5]，生产的产品总量为R，则总产量R在t时刻的产量，即微元dR=R′（t）dt=（50+5t-0.6t2）dt。因此，在[1，5]内总产量为

（二）压缩机做功问题

在生产生活过程中，压缩机做功问题由于关系到能源节约问题，因此备受大家关注。假设地面上有一个底半径为5 m，高为20 m的圆柱形水池，往里灌满了水。

如果要把池中所有的水抽出，则需要压缩机做多少功？此时，由于考虑到池中的水被不间断地抽出，可将抽出的水分割成不同的水层。

同时，把每层的水被抽出时需要的功定义为功微元。这样，该问题就可通过微元法解决了。

具体操作如下：将水面看做是原点所在的位置，竖直向下做x轴。当水平从x处下降了dx时，我们近似地认为厚度为dx的这层水都下降了x，因而这层水所做的功微元dw≈25πxdx（J）。当水被完全抽出，池内的水从20 m下降为 0 m。

根据微元法，压缩机所做的功为W=25πxdx=15708（J）。

（三）液体静压力问题

在农业生产过程中，为了保证农田的供水，常常需要建造各种储水池。因此，我们需要了解有关静压力问题。

在农田中有一个宽为 4 m，高为3 m，且顶部在水下 5 m的闸门，它垂直于水面放置。此闸门所受的水压力为多少？我们可以考虑将闸门分成若干个平行于水面的小长方体。

此时，闸门所受的压力可看做是小长方体所受的压力总和。当小长方体的截面很窄的情况下，可用其截面沿线上的压强来近似代替各个点处的压强。任取一小长方体，其压强可表示为1・x=x，长方体截面的面积为ΔA=4dx，从而ΔF≈x・4dx，

利用微元法求解定积分，还可以解决很多实际工程问题，关键是要掌握好换“元”的技巧。这就需要我们解决问题时，要特别注意思想方法。思想方法形式多种多样，如以直代曲、以均匀代不均匀、以不变代变化等。

参考资料：

百度百科-定积分

本图文由用户发布，该文仅代表作者本人观点，本站仅提供信息存储空间服务。如发现本站有涉嫌抄袭侵权/违法违规的内容，联系本站举报。转发注明出处：https://www.xsy-edu.com/n/72977.html

定积分公式运算法则(定积分四则运算法则)

定积分公式运算法则

定积分四则运算法则

定积分的基本运算法则

定积分的计算公式

相关推荐